Исследование управляемого движения самолета с помощью передаточный функций

При выполнении любой летной операции самолет последо­вательно осуществляет ряд режимов полета. Для перехода от одного режима к другому и для компенсации возмущений требуется управ­ление самолетом. Следовательно, самолет является объектом управ­ления.

Под управлением самолета понимается процесс формирования управляющих воздействий, обеспечивающий требуемый режим дви­жения.

Управляющие воздействия формируются на основе получения и обработки информации о характере движения самолета и заданной программы полета и осуществляются отклонениями органов управ­ления самолета и двигателя.

-Р*

Результат управления зависит от реакции самолета на управля­ющие воздействия, которая определяется его статическими и дина­мическими характеристиками и законом управления. Поэтому для оценки управляемости различных самолетов принято рассматривать их реакцию на скачкообразное (ступенчатое) отклонение органов управления и на отклонение по гармоническому закону.

При ступенчатом отклонении изучаются переходные или времен­ные характеристики (функции) самолета, а при гармоническом — частотные.

Частотными характеристиками системы (звена) называют за­висимость отношения амплитуды выходной величины к амплитуде входного сигнала и сдвига по фазе выходной величины по отношению к входному сигналу от частоты входного воздействия.

f Для самолета выходными величинами могут быть управляемые параметры движения (скорость, углы атаки, тангажа и. другие пере­грузки и т. п.), а входными — управляющие или возмущающие воздействия.

При изучении переходных характеристик (процессов) любой динамической системы (звена), описываемой линейными дифферен­циальными уравнениями с постоянными коэффициентами, удобно пользоваться передаточными функциями, а частотных характери­стик — частотными функциями.

Передаточной функцией называют отношение изображения вы­ходной величины к изображению входной при нулевых начальных условиях

(15.30)

Здесь Y (р) и X (р) — соответственно изображение по Лапласу выходной и входной величины. Двойной индекс WyX (р) указывает, что выходной величиной является у (/), входной — X (/).

Рассмотрим пример определения переходной функции звена с помощью его передаточной функции. Пусть это звено описывается линейным дифференциальным уравнением второго порядка с постоянными коэффициентами

Дg (/) + 2k Др (0 + со* Ду (Т) = К Ах (/)• (16.31)

Найдем передаточную функцию, соответствующую этому’ уравнению. Для этого определим изображения по Лапласу выходной Ду (Т) и входной. Ад (<) величии при нулевых начальных условиях.

Переходя от оригиналов Ду (0 и Ах (<) к их изображениям по формулам табл. 15.1 получим вспомогательное алгебраическое уравнение

(ра + 2hp + ша) ДК (р) = К ДХ(р). (15.32)

Откуда ДУ (р) = ^’ця > 8 передаточная функция

. Щ+Я—<“■“>.

Передаточную функцию можно рассматривать как удобную форму записи ли­нейных дифференциальных уравнений с постоянными коэффициентами, которая позволяет сравнительно просто исследовать динамические процессы.

Поскольку знаменатель передаточной функции составляется по левой — части уравнения, то ои является характеристическим полиномом дифференциального уравнения (15.31) с той лишь разницей, что вместо Я стоит параметр р.

Приравнивая нулю знаменатель передаточной функции (15.33), получим

р» + 2Лр + <о* = 0. (15.34)

Корин этого уравнения называются полюсами передаточной функции или корнями характеристического уравнения для системы (15.31).

Если (со* — Л*) > 0, то корни будут комплексными сопряженными

Р1, а = —Л ± 11Лв*^—ft5".

9 А. Ф. Бочкарев и др.

В этом случае будет колебательный процесс изменения выходной величины и звено является колебательным.

Если (ш2 — h2) < 0, то оба корня будут’“действительными р1>2 = — h ± ± h2 — <й2; процесс будет апериодическим, а звено — апериодическим второго порядка.

Выражая А К (р) через передаточную функцию (15.33), получим

ЛК (р) = Wvx (р) АХ (р) г pg — j — 2hp — V (о2 А* (Р)-

Для определения переходной (временной) функции надо за входное воздействие принять единичную ступенчатую функцию х (t) — 1 (<), изображение которой

X (р) = ——. Следовательно,

Р

Переходя при помощи таблиц от изображения к оригиналу для случая (со2—h2) > > 0, получим переходную функцию колебательного звена

„- к [і -+ , (15.37)

где К — передаточный коэффициент; h — коэффициент демпфирования; v = = Vыа — Л® — круговая частота колебаний; со — опорная частота или частота недемпфированных колебаний; сдвиг по фазе —

V (о2 —ha

ф = arctg v—j —. (15.38)

В (15.37) первое слагаемое определяет вынужденное движение, а второе — собственное (свободное) колебательное движение, определяющее переходной про­цесс.

Для определения реакции самолета на гармоническое воздействие рассматриваются линейные неоднородные уравнения с постоянными коэффициентами, правые части которых изменяются по гармониче­скому закону.

Входное гармоническое воздействие вызовет выходной процесс (возмущенное движение), состоящий из собственной и вынужденной составляющих.

В устойчивой системе собственная составляющая, определяемая из решения однородных уравнений, с течением времени затухает. Поэтому при изучении выходных процессов, вызванных гармониче­ским воздействием, ограничиваются только вынужденной состав­ляющей, предполагая, что система устойчива.

Вынужденная составляющая определяется как частное решение неоднородной системы уравнений. Если на вход системы (звена) подается гармонический сигнал Ах (() = Ах sin со(, то на выходе вынужденная составляющая будет изменяться по гармоническому закону с той же частотой со, но с другой амплитудой и со смещением по фазе

Ay (t) = Ai sin (to(+ у), (15.39)

где А2 и to — амплитуда и частота вынужденных колебаний выходной величины; у — сдвиг по фазе.

Величины А2 и у весьма просто определяются по частотной функ­ции W (ito), представляющей собою комплексную величину.

Можно показать, что W (itо) получается из передаточной функ­ции W (р) (15.30) путем замены р = itо, где to— частота вынужден­ных колебаний.

Частотную функцию можно представить в виде

W (itо) = Re (to) — f — і Іш (to) — A (to) е(т, (15.40)

где Re (to), Im (to) — соответственно вещественная и мнимая часть частотной функции; A (to) = — | W (ito) | — модуль частотной

функции, называется амплитудно-частотной характеристикой (АЧХ); v (to) — arg W (ito) — аргумент частотной функции, назы­вается фазовой частотной характеристикой (ФЧХ).

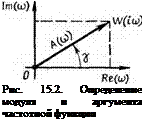
Для определения модуля и аргумента частотной функции изо­бразим W (itо) на комплексной плоскости для одного значения to (рис. 15.2).

Из рис. 15.2 видно, что

A (to) = = /Re2 (to) + Іш2 (to), (15.41)

?=агсі£тШг (15-42)

С помощью этих выражений можно строить амплитудную и фазовую частотные характеристики системы (звена) при изменении частоты вынужденных колебаний to от 0 до +оо..

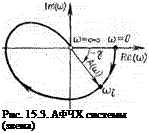
Кроме этих характеристик можно построить амплитудио-фазовую частотную характеристику (АФЧХ), представляющую собой кривую на комплексной плоско­сти, по которой перемещается конец вектора частотной функции W (ito) при изме­нении частоты входного сигнала to от 0 до оо.

Для построения АФЧХ надо для каждого значения частоты вычислить по фор­мулам (15.41) и (15.42) A (to) и у (to). Затем иа комплексной плоскости под углом у из начала координат провести луч, на котором отложить значение A (to). Совокуп­ность точек образует АФЧХ системы (звена) — рис. 15.3.

АФЧХ так же как передаточная функция W (р) и дифференциальное урав­нение системы (звена) определяет ее динамические свойства, но обладает тем пре­имуществом, что может быть построена экспериментально.

Частотный метод анализа для линейных систем широко при­меняется в теории автоматического управления и динамике управ­ляемого движения самолета. В дальнейшем при изучении реакции

самолета на управляющие и возмущающие воздействия будем ис­пользовать передаточные функции и частотные характеристики само­лета.

До сих пор рассматривались системы линейных дифференциаль­ных уравнений с постоянными коэффициентами.

В случае неустановившегося опорного движения системы ли­нейных дифференциальных уравнений (15.9) и (15.10) будут с пере­менными коэффициентами. Интегрирование таких систем можно проводить численными методами на ЭВМ. Для получения аналити­ческого решения задачи в инженерной практике иногда пользуются приближенным методом «замороженных коэффициентов». Сущность этого метода состоит в том, что отрезок времени t, в течение которого происходит исследуемое движение, разбивается на отдельные интер­валы. На этих интервалах коэффициенты уравнений принимаются постоянными и равными их значениям в начале интервала. Тогда математически задача будет описываться совокупностью систем дифференциальных уравнений с постоянными коэффициентами. Число таких систем равно числу интервалов времени. Однако о до­пустимости этого метода с достаточной для практики достовер­ностью можно судить только после анализа конкретных характе­ристик летательного аппарата и систем стабилизации на основании численного интегрирования уравнений с переменными коэффициен­тами с помощью вычислительной техники.

Дополнительная литература

191 с. 228, [И ] с. 180-209, [8І с. 234-246.

Контрольные вопросы

1.Какова методика линеаризации нелинейных уравнений возмущенного дви­жения? Проведите линеаризацию одного цз нелинейных уравнений возмущенного движения самолета.

2. При каких условиях возможно разделение линейных уравнений возмущен­ного движения самолета?

3. Каковы метематические методы исследования динамики возмущенного дви­жения самолета?

4. Когда линейные уравнения полностью решают задачу об устойчивости и неустойчивости иевозмущеииого движения?

5. Сформулируйте алгебраический критерий устойчивости.